Answer:
This is a question from Ratio and Proportion based concept.
Given that,
120 men working for 9 hours a day, construct a road in 40 days. We are required to calculate the number of days to construct the road if 150 people work for 6 hours.
Let's assume the number of days taken for constructing is 'x'.
So normally we take 2 ratios and obtain the unknown value by cross multiplication.
Applying the same approach we get:
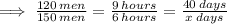
Since the first two fractions are inversely related, we multiply the numerators and denominators respectively.
Hence we get:

Hence it takes 33.33 days for 150 men to construct the road working for 6 hours each day.