Question

Find the exact lengths of the sides of quadrilateral ABCD with vertice

A(4, 5), B(-3, 3), C(-6, -13) and D(6, - 2).

Answer 1

`AB=√(53)`

`BC=√(265)`

`CD=√(265)`

`DA=√(53)`

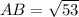
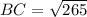
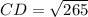
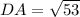
ABCD is a kite.

Explanation:

Given vertices of quadrilateral ABCD:

• A = (4, 5)
• B = (-3, 3)
• C = (-6, -13)
• D = (6, -2)

To find the exact lengths of the sides of the quadrilateral, use the distance formula.

`\boxed{\begin{minipage}{7.4 cm}\underline{Distance between two points}\\\\$d=√((x_2-x_1)^2+(y_2-y_1)^2)$\\\\\\where $(x_1,y_1)$ and $(x_2,y_2)$ are the two points.\\\end{minipage}}`

`\begin{aligned}AB&=√((x_B-x_A)^2+(y_B-y_A)^2)\\&=√((-3-4)^2+(3-5)^2)\\&=√((-7)^2+(-2)^2)\\&=√(49+4)\\&=√(53)\\\end{aligned}`

`\begin{aligned}BC&=√((x_C-x_B)^2+(y_C-y_B)^2)\\&=√((-6-(-3))^2+(-13-3)^2)\\&=√((-3)^2+(-16)^2)\\&=√(9+256)\\&=√(265)\\\end{aligned}`

`\begin{aligned}CD&=√((x_D-x_C)^2+(y_D-y_C)^2)\\&=√((6-(-6))^2+(-2-(-13))^2)\\&=√((12)^2+(11)^2)\\&=√(144+121)\\&=√(265)\\\end{aligned}`

`\begin{aligned}DA&=√((x_A-x_D)^2+(y_A-y_D)^2)\\&=√((4-6)^2+(5-(-2))^2)\\&=√((-2)^2+(7)^2)\\&=√(4+49)\\&=√(53)\\\end{aligned}`

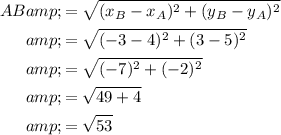
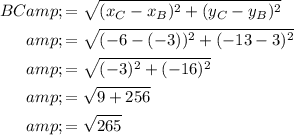
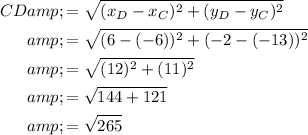
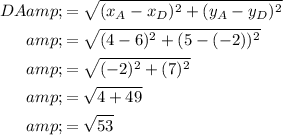
A kite has two pairs of adjacent equal sides.

Therefore, quadrilateral ABCD is a kite as:

• AB is adjacent to DA and AB = DA.
• BC is adjacent to CD and BC = CD.