Question

The graph shows the height y in feet of a balloon that is launched from a platform 13.5 feet high as a quadratic function of x the time in seconds

what is the domain of this function in this situation?

Answer 1

Domain is 0 ≤ x ≤ 54

Interval notation: [0, 54]

Explanation:

I am a little confused by the question and even more so when I look at the answer choices you provided as a comment.

The domain of any function y = f(x) is the range of values of x that result in a defined real value for y.

Your answers provide the choices as single values which is not correct

Let's find the equation of the quadratic function y = f(x)

Given a vertex (h, k) , the quadratic equation is

`y = a(x - h)^2 + k\\\\`

Here we have h = 24.5 and y = 43.5

So the equation is

`y = a(x - 24.5)^2 + 43.5\\\\`

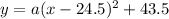
To find a, plug in coordinates of a point on this quadratic function from the graph. We see the function has (0, 13,5) as a point

So:

`13.5 = a(0-24.5)^2 + 43.5\\\\13.5 = a(-24.5)^2 + 43.5\\\\a = (-30)/((-24.5)^2)\\\\\\\textrm{which results in }\\a = -0.05 (rounded)`

We can find the x-intercepts of this parabola which are the domain values by plugging in 0 for y and solving for x

`0 = -0.05(x-24.5)^2 + 43.5\\\\-0.05(x - 24.5)^2 = -43.5\\\\(x - 24.5)^2 = (-43.5)/(-0.05) = 870\\\\\\x - 24.5 = \pm √(870)\\\\x - 24.5 = \pm 29.5\\x = 24.5 \pm 29.5\\\\x = (-5, 54)\\\\`

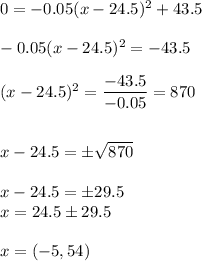
So this should be the domain of x; Note however, that we cannot have negative values for x and the parabola graph does show it starts at x = 0

Domain of this function is 0 ≤ x ≤ 54

which is written in interval notation as

[0, 54]