Answer:
g(x) = (
 )/3 + 5
)/3 + 5
Explanation:
f(x) =
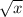 + 5
+ 5
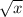 + 5 ==> 1/3 *
+ 5 ==> 1/3 *
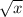 + 5 ==> vertical shrink is when the function's y-coordinates shrink from the y-intercept (5 is the y-int) by a factor of 1/3
+ 5 ==> vertical shrink is when the function's y-coordinates shrink from the y-intercept (5 is the y-int) by a factor of 1/3
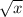 /3 + 5 ==>(
/3 + 5 ==>(
 )/3 + 5 ==> in order to translate the graph 3 units to the right, subtract x by 3 since x is being affected when the graph moves left/right. In addition, x now has to be 3 units greater in order for the function to have the same value:
)/3 + 5 ==> in order to translate the graph 3 units to the right, subtract x by 3 since x is being affected when the graph moves left/right. In addition, x now has to be 3 units greater in order for the function to have the same value:
 =
=

4 > 1 and 4 = 1 + 3
Hence, g(x) = (
 )/3 + 5
)/3 + 5