Question

Evaluate the square root of 9 + 4√5 in the form c + √d​

Answer 1

Explanation:

Here we are interested in finding the square root of
`9 +4\sqrt5` . So , we have

`\longrightarrow √( 9+4\sqrt5)`

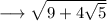
We can write it as ,

`\longrightarrow √( 5 + 4 + 4\sqrt5)`

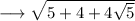
This can be again rewritten as ,

`\longrightarrow√( (\sqrt5)^2+2^2+ 2(2)(\sqrt5) )`

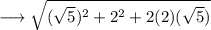
Now this in the form of
`a^2+b^2+2ab` form which is the square of
`(a+b)` . So that,

`\longrightarrow √( (2+\sqrt5)^2)`

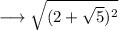
Simplify the root ,

`\longrightarrow 2 + \sqrt5`

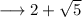
Hence we got our answer in the form of
`c +√(d)`

And we are done!

—Rishabh