Question

The lines shown below are perpendicular. Find the slope-intercept form of the equation of line y2.

y2

(-3,7)


Y₁ = 3x-6

Answer 1

`y2 = -(1)/(3)x + 6`

Explanation:

Perpendicular lines have slopes that when multiplied will result in a value of -1

In other words, the slope of y2 = - 1/(slope of y1)

y1 = 3x - 6
Slope of y1 = 3

So slope of y2 = -1/3

Equation of y2 is of the form

`y_2 = -(1)/(3)x_2 + b`

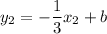
The line passes through (-3, 7)

To find b plug in y2 = 7, x2 = -3 into the above equation and solve for b

`7 = -(1)/(3)(-3) + b`

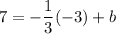
=> 7 = 1 + b

b = 7-1 = 6

So the equation of line y2 is

`y2 = -(1)/(3)x + 6`

Hint: If you look at the graph, line y2 crosses at b = 6

We need not have used equations to solve for b but we have to be careful. We can at least the graph value to see if our b value is close to it