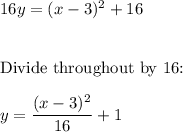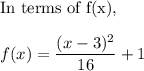Question

The vertex of a parabola is at the point (3,1), and its focus is at (3,5). What function does the graph represent?

A. f(x)=(x - 3)² - 1
B. f(x)=(x + 3)² - 1
C. f(x)=(x - 3)² - 1
D. f(x) = (x - 3)² + 1

Answer 1

`\textrm{In terms of f(x),}\\\\f(x) = ((x-3)^2)/(16) + 1\\\\`

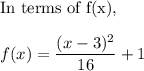
Unable to match any of the answer choices provided. There has to be a mistake in the typing of the answer choice equations

Explanation:

The equation of a vertical upward parabola given vertex (h, k) and focus(f, k) is :

(x-h)² = 4a(y-k)

a is the vertical distance between the y-coordinate of the focus and the y-coordinate of the vertex

The given parameters are vertex = (h, k) with h = 3, k = 1

Focus is (f, k) with f = 3, k = 5
(y-coordinate of a vertical parabola's vertex = y-coordinate of its focus)

a = 5- 1 = 4

Apply the equation:

`(x-h)^2 = 4a(y-k)\\\\(x - 3)^2= 4\cdot4(y - 1)\\\\(x - 3)^2= 16(y - 1)\\\\(x - 3)^2= 16y - 16\\\\`

Switch sides and add 16 to both sides:

`16y = (x-3)^2 + 16\\\\\\\textrm{Divide throughout by 16:}\\\\y = ((x-3)^2)/(16) + 1\\\\`

`\textrm{In terms of f(x),}\\\\f(x) = ((x-3)^2)/(16) + 1\\\\`