Answer:
For less than 50 calls, option 1 is the best, while for more than 50 calls, option 2 is the best.
Explanation:
Option 1:
For n calls, the cost is given by:
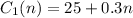
Option 2:
The cost is flat of 40, so
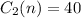
Which plan is the best option?
Depends on the number of calls, as for a high number,
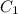 will be higher than
will be higher than
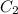 . We have to find this number. So
. We have to find this number. So
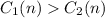
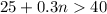

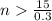
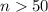
This means that for less than 50 calls, option 1 is the best, while for more than 50 calls, option 2 is the best.