Question

Question
Graph the solution to this inequality on the number line.

−16≥−4p

Answer 1

The answer is:

4 ≤ p

Work/explanation:

The inequality is:

`\sf{-16\geqslant-4p}`

To solve, divide each side by -4. Since we're dividing by a negative number, we will reverse the inequality sign.

We end up with:

`\sf{4\leqslant p}`

Hence, the answer is 4 ≤ p.

Answer 2

Attached,
`p \geq 4`

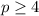
Knowledge Needed

To solve, you must isolate the variable. It means moving the variable and it's coefficient to the other side of the equation by itself.

Rule

If you multiply, divide, add, subtract, square root, exponent both sides of the equation by the same value, that end value stays the same. That is how you solve for it.

However, if you divide or multiply by a negative number by both sides in an inequality, you must flip the sign.

For example:

> to <

to

Question

Divide -4 on both sides.

`(-16)/(-4) \geq (-4p)/(-4)`

`4 \geq p`

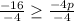
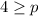
Flip the sign.

`4\leq p`

`p\geq 4`

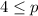
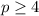
When the line is pointing right, it means the variable is greater than the said number. If the dot is filled in, it means greater than or equal to or less than or equal to. If it is not filled in, it means greater than or less then.