Given:
The compound inequality is
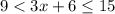
To find:
The solution for the given compound inequality in interval notation.
Solution:
We have,
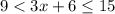
Subtracting 6 from each side, we get
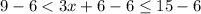
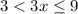
Divide each side by 3.
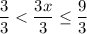
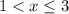
Here, 1 is not included in the solution set and 3 is included in the solution set.
Therefore, the solution in interval notation is (1,3].