Question

Line p is perpendicular to q where the equation of q is 4x-6y=24. Line p also passes through the point (-2,5). Determine the equation of pin point slope form.

Answer 1

We need to determine the equation of the line in point-slope form, which is shown below:

`y-y_0=m\cdot(x-x_0)`

Where (x0, y0) is a point that belongs to the line, and m is the slope.

The first step we need to take, is to determine the slope of the line given to us, which is done below:

`\begin{gathered} 4x-6y=24 \\ -6y=24-4x \\ y=(4)/(6)x-4 \end{gathered}`

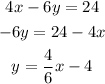
The slope for this line is 4/6. We want to determine the line that is perpendicular to it, which means we have to find the slope the negative reciprocal to this slope, which is done below:

`\begin{gathered} m_2=-(1)/(m_1) \\ m_2=-(1)/((4)/(6)) \\ m_2=-(6)/(4) \\ m_2=(-3)/(2) \end{gathered}`

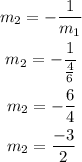
The slope of the perpendicular line is -3/2. The point we need is (-2, 5), therefore the equation is:

y-5=-1.5*(x- (-2) )