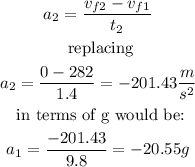Question

Dr. John Paul Stapp was a U.S. Air Force officer who studied the effects of extreme deceleration on the human body. On December 10, 1954, Stapp rode a rocket sled, accelerating from rest to a top speed of 282 m/s (1015 km/h) in 5.00 s, and was brought jarringly back to rest in only 1.40 s!Calculate the magnitude of the average acceleration during the first part of his motion and the magnitude of the average acceleration during the second part of his motion?

Answer 1

a. 5.75g

b. -20.55g

Explanation:

We have the following information from the statement:

`\begin{gathered} v_i=0\text{ m/s} \\ v_(f1)=282\text{ m/s} \\ v_(f2)=0\text{ m/s} \\ t_1=5\text{ s} \\ t_2=1.4\text{ s} \end{gathered}`

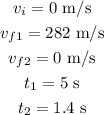
To calculate the acceleration during the first part of the motion it would be:

`\begin{gathered} a_1=(v_f-v_i)/(t_1) \\ \text{ replacing} \\ a_1=(282-0)/(5)=56.4(m)/(s^2) \\ \text{ in terms of g would be:} \\ a_1=(56.4)/(9.8)=5.75g \end{gathered}`

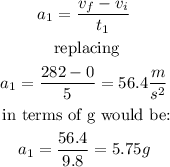
To calculate the acceleration during the second part of the movement it would be:

`\begin{gathered} a_2=(v_(f2)-v_(f1))/(t_2) \\ \text{ replacing} \\ a_2=(0-282)/(1.4)=-201.43(m)/(s^2) \\ \text{ in terms of g would be:} \\ a_1=(-201.43)/(9.8)=-20.55g \end{gathered}`