Answer:
Explanation:
In order to find the coordinates of P and Q, we have to find the intersection of the circle and the line. Do this by subbing in y=x-4 into the circle equation for y:
 becomes
becomes
 and then FOIL all that out to get
and then FOIL all that out to get
 . Combine like terms to get
. Combine like terms to get
 and factor to get the zeros of
and factor to get the zeros of
x = 6 and x = -1.
When x = 6, y = 2; when x = -1, y = -5. That answers part a.
The length of PQ is found then using the distance formula:
 to get
to get
 which, in decimal form, i 9.89949937. That answers part b.
which, in decimal form, i 9.89949937. That answers part b.
The perpendicular bisector requires that we find the midpoint of PQ:
 which, for us, is
which, for us, is
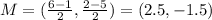
The perpendicular slope to the given line is the opposite reciprocal of the one given, so the perpendicular slope is -1. The equation for the perpendicular bisector of PQ goes through the midpoint with the slope of -1:
 and
and
y = -x + 1 is the perpendicular bisector of PQ.