Answer:
To find the value of the integral of
 from 0 to 2, we need to evaluate the definite integral:
from 0 to 2, we need to evaluate the definite integral:
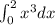
Using the power rule of integration, we can integrate the function as follows:
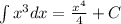
where C is the constant of integration.
Plugging in the limits of integration, we get:
![\int_(0)^(2) {x}^(3) dx = \left[\frac{{x}^(4)}{4}\right]_(0)^(2)](https://img.qammunity.org/2024/formulas/mathematics/high-school/1oozwuq9r3sa1d4bg5zjxt9gnbij4o53zs.png)
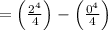

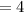
Therefore, the value of the integral of
 from 0 to 2 is 4.
from 0 to 2 is 4.