Question

Decide whether it is an even function, an odd function, or neither

Answer 1

Given:

There are 2 graphs and 2 functions given in the question

Required:

We need to identify that which are even and which are odd

Step-by-step explanation:

Even function:

f(-x) = f(x)

The graph of an even function is symmetric with respect to the y-axis.

Odd function:

f(-x) = -f(x)

The graph of an odd function is symmetric with respect to the origin

Here 1st graph is neither even nor odd function because it is not symmetric with respect to the y-axis and also not symmetric with respect to the origin

2nd graph is even because it is

1st function is neither even nor odd because

`f(-x)=-6(-x)^5+7x^2=6x^5+7x^2\\e-f(x)`

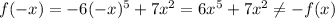
2nd function is