Step 1:
Define mean, median, and mode.
The arithmetic mean is found by adding the numbers and dividing the sum by the number of numbers in the list. ... This is what is most often meant by an average. The median is the middle value in a list ordered from smallest to largest. The mode is the most frequently occurring value on the list.
Step 2
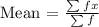
Step 3
x f fx
2 3 6
3 9 27
4 4 16
5 1 5
6 8 48
7 4 28
8 3 24
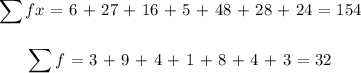
Step 4:
Find the mean
![\begin{gathered} \text{Mean = }(154)/(32) \\ \operatorname{mean}\text{ = 4.8125 }\approx\text{ 5} \end{gathered}]()
Step 5
To find the median, first the position of the median.
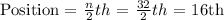
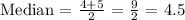
Step 6
mode = 3