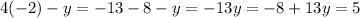Answer:
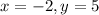
Explanation:
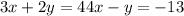
Take either of the equations and choose which to make the subject. i shall choose the second equation and make -y the subject of the formula.
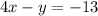
lets take -y to the other side because we want -y to be positive, ie (+y)
 take -13 to the other side,
take -13 to the other side,
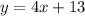
now that we have that we take the other equation and substitute what y is into the equation, i.e
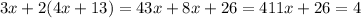
we take +26 to the other side,
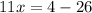

 divide both sides by 11, x becomes
divide both sides by 11, x becomes

now that we know what x is we substitute it into the formula,