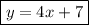Question

What is an equation of the line that passes through points (-1,3) and (-2,-1)?

Answer 1

`\boxed{y = 4x + 7}`

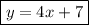
Explanation:

The equation of a line in slope-intercept form is

y = mx + b

where m is the slope and b the y-intercept

To find the slope, take the two points, find the difference in y values and divide by the corresponding difference in x values

Two points are
`(- 1, 3)` and
`(- 2, -1)`

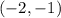
Difference in y values
`= -1 -3 = -4`

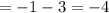
Difference in corresponding x values
`= -2 - (-1) = -2 + 1 = -1`

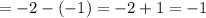
Slope

`m = (-4)/(-1) = 4`

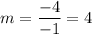
So the equation of the line is of the form

`y = 4x + b`

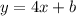
To find b, take the coordinates of any of the two points and plug the x and y values into the above equation and solve for b

Let's take point (-1, 3)

Plug in values:

`3 = -4 + b\\\\3+4 = b\\ \\b = 7`

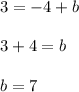
Therefore the equation of the line is

`\boxed{y = 4x + 7}`