Question

Find two monomials whose product equals -20a^4b², and whose sum is a monomial with a coefficient of 1.

Answer 1

-4a²b

5a²b

Explanation:

A monomial is a polynomial that has one term only but can have multiple variables.

Given monomial:

`-20a^4b^2`

The coefficient of the given monomial is -20.

Therefore, we need to find two numbers that multiply to -20 and sum to 1.

Factors of -20:

• -1 and 20
• -2 and 10
• -4 and 5
• -5 and 4
• -10 and 2
• -20 and 1

Therefore, the two numbers that multiply to -20 and sum to 1 are:

• -4 and 5

Rewrite -20 as the product of -4 and 5:

`\implies -4 \cdot 5 \cdot a^4b^2`

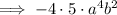
Rewrite the exponents as sums of equal numbers:

`\implies -4 \cdot 5 \cdot a^(2+2) \cdot b^(1+1)`

`\textsf{Apply exponent rule} \quad a^(b+c)=a^b \cdot a^c`

`\implies -4 \cdot 5 \cdot a^2 \cdot a^2\cdot b^(1)\cdot b^(1)`

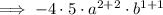
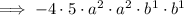
Rearrange as the product of two monomials with the same variables:

`\implies -4a^2 b^(1)\cdot 5 a^2 b^(1)`

`\implies -4a^2 b\cdot 5 a^2 b`

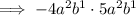
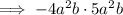
Therefore, the two monomials whose product equals -20a⁴b², and whose sum is a monomial with a coefficient of 1 are:

• -4a²b
• 5a²b

Check the sum of the two found monomials:

`\begin{aligned}\implies -4a^2b+5a^2b&=(-4+5)a^2b\\&=(1)a^2b\\&=a^2b\end{aligned}`

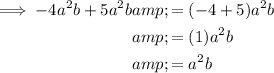
Thus proving that the sum of the monomials has a coefficient of 1.