Question

Consider the quadratic equation x squared minus 7 x minus 18 equals 0

Find the solutions by factoring.


x = -9, x = 2


x = -2, x = 9


x = -6, x = 3


x = -3, x = 6

Answer 1

x = -2, x = 9

Explanation:

Given quadratic equation:

`x^2-7x-18=0`

To factor a quadratic in the form ax²+bx+c, first find two numbers that multiply to ac and sum to b.

`\implies ac=1 \cdot -18=-18`

`\implies b=-7`

Therefore, the two numbers are: -9 and 2.

Rewrite b as the sum of these two numbers:

`\implies x^2-9x+2x-18=0`

Factor the first two terms and the last two terms separately:

`\implies x(x-9)+2(x-9)=0`

Factor out the common term (x - 9):

`\implies (x+2)(x-9)=0`

Apply the zero-product property:

`\implies x+2=0 \implies x=-2`

`\implies x-9=0 \implies x=9`

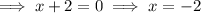
Therefore, the solutions to the given quadratic equation are:

• x = -2, x = 9