Question

[(1/15−2/5)⋅(−3/4)³]÷(−9)

Answer 1

`-(1)/(64)`

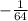
Explanation:

We have:

`[( (1)/(15) - (2)/(5)) * (-(3)/(4))^(3)] / (-9)`

Now, we will multiply the second fraction in the first parentheses by
`(3)/(3)` so we can subtract it from the
`(1)/(15)`. Then, we will multiply all of the
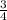`(3)/(4)`'s. This gives us:

`[( (1)/(15) - (2)/(5) * (3)/(3) ) * (-(3)/(4) * -(3)/(4) * -(3)/(4))] / (-9)`

Which simplifies to:

`[( (1)/(15) - (6)/(15) ) * (-(27)/(64))] / (-9)`

Simplifying:

`[(-(5)/(15) ) * (-(27)/(64))] / (-9)`

Multiplying in our brackets gives us:

`(9)/(64) / (-9)`

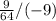
Now, using the rule of KCF (Keep, Change, Flip), we will keep our first fraction, change our division sign to a multiplication sign, and make the last number its reciprocal. This gives us:

`(9)/(64) * -(1)/(9) = -(1)/(64)`

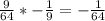
So, the equation simplified is
`-(1)/(64)`.

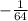Hope this helped!