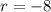Question

M varies jointly as r² and as l. If M = 20 when I = 8 and r = 2, find: (a) the law connecting these variables, (b) r when M = 400 and l=10.​

Answer 1

(a) Law connecting the variables:

`M = (5)/(8)Ir^(2)`

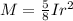
(b) r = 8 and r = -8

Explanation:

(a) Equation for a joint variation is:

`M = KIr^(2)` where K is the constant

Substituting the provided values of M, I and r:

=
`20 = K(8)(2^(2) )`

=
`20 = K(8)(4)`

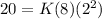
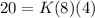
= 20 = 32K

=
`K = (20)/(32)`

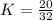
[Divide the numerator and the denominator by the highest common factor (i.e. 4)]

=
`K = (5)/(8)`

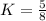
Therefore:

`M = (5)/(8)Ir^(2)`

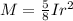
(b)
`M = (5)/(8) I r^(2)`

Substituting the values of M and I:

`400 = (5)/(8) (10)r^(2)`

`400 = (5)/(8) (10)r^(2)`

`400 = (50)/(8) r^(2)`

`((400)(8))/(500) =r^(2)`

`(3200)/(50) = r^(2)`

`64 =r^(2)`

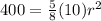
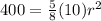
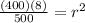
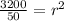
Taking the square root on both sides of the equation:

`r = √(64)`

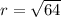
`r = 8` and
`r = -8`