Question

A region satisfies the inequalities 1 ≤ x ≤ 5 and 2 ≤ y ≤a. What value of a would give the region an area of 24 square units?​

Answer 1

a = 8

Explanation:

The following inequalities will form a rectangle. Hence, the area of a rectangle is
`\displaystyle{A=\Delta x \cdot \Delta y}`

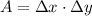
In this case,
`\Delta x` = 5-1 which is 4, and
`\Delta y` = a - 2. Substitute in:

`\displaystyle{24 = 4\cdot (a-2)}`

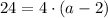
Now solve the equation for a-term:

`\displaystyle{24=4a-8}\\\\\displaystyle{24+8=4a}\\\\\displaystyle{32=4a}\\\\\displaystyle{8=a}`

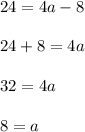
Therefore, the value of a is 8 to make the region have an area of 24 square units.