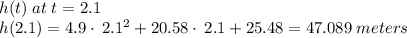Question

A ball is launched from a 25.48-meter tall platform. The equation

for the ball's height h at time t seconds after launch is h (t) =
-4.9t2 +20.58t + 25.48, where his in meters. What is the
maximum height the ball achieves before landing?

Answer 1

`\boxed{47.089 \;meters} \\\\`

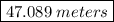
Explanation:

For any function f(x), the maximum or minimum value can be determined by 1. Finding the first derivative f(x) with respect to x i.e. f'(x)

2. Setting this first derivative to 0, solving for x

3. Substituting for x in the original function to get the maximum/minimum value

`\textrm{The equation for the function f(t) is }\\f(t) = -4.9t^2 + 20.58t + 25.48\\\\`

`\textrm{The first derivative of this function with respect to t is }\\\\f'(t) = - 2\cdot 49t + 20.58\\= -9.8t + 25.48\\\\`

`\textrm{Setting this first derivative equal to 0 gives:}\\\\-9.8t + 20.58 = 0\\\\-9.8t = -20.58 \;\;\;\;\;\textrm{(Subtracting 20.58 from both sides)}\\\\9.8t = 20.58 \;\;\;\;\;\; \textrm{ (Multiplying both sides by -1)}`

`\textrm{Therefore }\\\\t = (20.58)/(9.8)\\\\t= 2.1 \textrm{ seconds}`

`\textrm{Therefore, at = 2.1 seconds, the ball will reach its maximum height.}`

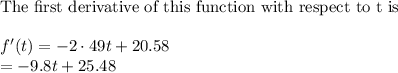
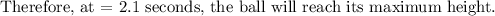
To find what this maximum height is, substitute t = 2.1 in the original equation and solve for h(t)

`h(t)\;at\;t=2.1 \\h(2.1) = 4.9\cdot \:2.1^2+20.58\cdot \:2.1+25.48=47.089 \;meters\\\\`

`\textrm{ The maximum height the ball achieves before landing is } \boxed{47.089 \;meters} \\\\`

`\textrm {This occurs 2.1 seconds after launch }`