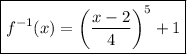Answer:
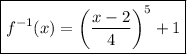
This is the last choice on the screenshot you provided
Explanation:
Use y to represent f(x)
![y=4\sqrt[5]{x-1}+2](https://img.qammunity.org/2024/formulas/mathematics/high-school/vqeduynv4bslkyqvmhobfyw19kqyffmjy6.png)
Replace x with y and y with x:
![x=4\sqrt[5]{y-1}+2](https://img.qammunity.org/2024/formulas/mathematics/high-school/onp9zweiats556zoerkq4aqth9e7xkaje8.png)
Solve for y in terms of x and that will be the inverse of f(x)
- Switch sides:
![4\sqrt[5]{y-1}+2=x](https://img.qammunity.org/2024/formulas/mathematics/high-school/f8929ejghsn3q95jykcvgv4mahy9ylydod.png)
- Subtract 2 from both sides:
![4\sqrt[5]{y-1}=x-2](https://img.qammunity.org/2024/formulas/mathematics/high-school/ma5ydzxpr49ci7t9lnyxciu5hs3fpbvc02.png)
- Divide both sides by 4
![\sqrt[5]{y-1}=(x-2)/(4)](https://img.qammunity.org/2024/formulas/mathematics/high-school/6315p74qwi4xbqf5c3hh1hgguhxvbxs02h.png)
- Raise both sides to the 5th power to get rid of the radical
![\displaystyle \left(\sqrt[5]{y-1}\right)^5=\left((x-2)/(4)\right)^5](https://img.qammunity.org/2024/formulas/mathematics/high-school/8xq9gjaqere660e99g6n4kmovq4znfzw8n.png)
- This works out to
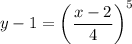
- Simplifying we get
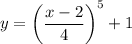
- The right side is the inverse of f(x)
Answer: Last choice on the screen, namely