Question

Please answer all parts of the questions and show all work. Be sure to show all steps.

Answer 1

• (a)See graph below

,

• (b)The rock will be 258 feet high at t=2.39 seconds and at t=3.61 seconds.

Explanation:

Given the equation modeling the height, h(t) of the rock after t seconds:

`h(t)=-16t^2+96t+120`

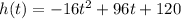
Part A

To sketch the graph, we use the intercepts and the vertex.

When t=0:

`\begin{gathered} h(0)=-16(0)^2+96(0)+120 \\ h(0)=120\text{ feet} \\ \implies(0,120) \end{gathered}`

The y-intercept is (0,120)

When h(t)=0:

`\begin{gathered} h(t)=-16t^2+96t+120=0 \\ \text{ We solve for t using the quadratic formula} \\ t=(-b\pm√(b^2-4ac) )/(2a) \\ t=(-96\pm√(96^2-4(-16)(120)))/(2(-16))=(-96\pm√(16896))/(-32) \\ t=(-96+√(16896))/(-32)\text{ or }t=(-96-√(16896))/(-32) \\ t=-1.06\text{ or }t=7.06 \end{gathered}`

The only possible x-intercept is (7.06, 0).

To find the vertex, we use the vertex formula below:

`\begin{gathered} (h,k)=\left(-(b)/(2a),(4ac-b^2)/(4a)\right) \\ =\left(-(96)/(2(-16)),(4(-16)(120)-96^2)/(4(-16))\right) \\ =(3,264) \end{gathered}`

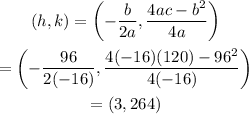
Use these points to sketch the graph as shown below:

Part B

When the rock is 258 feet high: h(t)=258

`\begin{gathered} -16t^2+96t+120=258 \\ -16t^2+96t+120-258=0 \\ \implies-16t^2+96t-138=0 \end{gathered}`

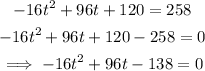
We solve the equation for t:

`\begin{gathered} \text{ We solve for t using the quadratic formula} \\ t=(-b\pm√(b^2-4ac) )/(2a) \\ a=-16,b=96,c=-138 \\ t=(-96\pm√(96^2-4(-16)(-138)))/(2(-16))=(-96\pm√(384))/(-32) \\ t=(-96+√(384))/(-32)\text{ or }t=(-96-√(384))/(-32) \\ t=2.39\text{ or }t=3.61 \end{gathered}`

The rock will be 258 feet high at t=2.39 seconds and at t=3.61 seconds.