Answer:
• (a)See graph below
,
• (b)The rock will be 258 feet high at t=2.39 seconds and at t=3.61 seconds.
Explanation:
Given the equation modeling the height, h(t) of the rock after t seconds:
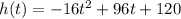
Part A
To sketch the graph, we use the intercepts and the vertex.
When t=0:
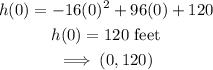
The y-intercept is (0,120)
When h(t)=0:
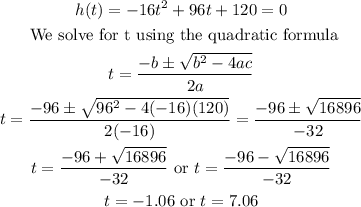
The only possible x-intercept is (7.06, 0).
To find the vertex, we use the vertex formula below:
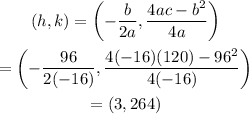
Use these points to sketch the graph as shown below:
Part B
When the rock is 258 feet high: h(t)=258
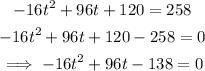
We solve the equation for t:

The rock will be 258 feet high at t=2.39 seconds and at t=3.61 seconds.