Question

A small city has a population of 34000 in 1994. The population growth after 1994 is modeled by the following function where is the number of years after 1994.

P(t)=34000e 0.04t
During what year will the population reach 68000?

Answer 1

`P(t)=3400e^(0.04t)\implies 68000=3400e^(0.04t)\implies \cfrac{68000}{3400}=e^(0.04t) \\\\\\ 20=e^(0.04t)\implies \log_e(20)=\log_e(e^(0.04t))\implies \log_e(20)=0.04t \\\\\\ \ln(20)=0.04t\implies \cfrac{\ln(20)}{0.04}=t\implies 74.89\approx t`

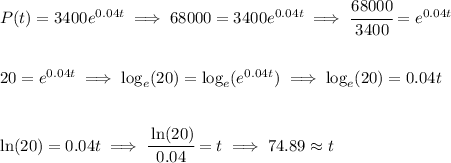
that's about 74 years and 325 days more or less.

based on the exponential equation which is really a continuously compounding equation with an initial value of 34000 in 1994, so 74 years later that'd be 1994 + 74 = 2068, then we add the 325 days to that, well, that's pretty much in November in 2069.