Question

Write the equations for the lines parallel andperpendicular to the given line j that passesthrough Q. 26. y = - 4x + 1; Q(6, -1)

Answer 1

We are given the following:

`\begin{gathered} y=-4x+1 \\ It\text{ passes through Point Q} \\ Q(6,-1) \end{gathered}`

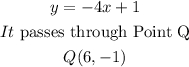
The general equation of a linear function is given by:

`\begin{gathered} y=mx+b \\ where\colon m=slope,b=y-intercept \end{gathered}`

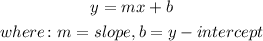
From the equations above, we deduce that:

`\begin{gathered} y=-4x+1 \\ \Rightarrow m=-4 \\ \Rightarrow b=1\ln \\ \\ \therefore Slope(m)=-4,y-intercept(b)=1_{} \end{gathered}`

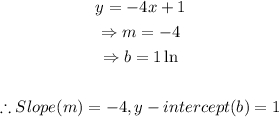
Two lines are considered parallel if they have an equal slope/gradient

We were given the Point Q. We will proceed to substitute the value of Q into the equation of the line. We have:

`\begin{gathered} y=mx+b \\ (x,y)=Q(6,-1) \\ \Rightarrow-1=-4(6)+b \\ -1=-24+b \\ \text{Add ''-2'' to both sides, we have:} \\ 23=b \\ b=23 \\ \text{Substitute the value of ''b'' into the }original\text{ equation, we have:} \\ y=-4x+23 \\ \\ \therefore The\text{ equation of the parallel line is }y=-4x+23 \end{gathered}`

Therefore, the quation of the parallel line is }= - 4x+ 2 3$

Two lines are considered to be perpendicular if their slopes are the negative reciprocal of one other

Mathematically represented as:

`\begin{gathered} m(perpendicular)=-(1)/(m) \\ m=-4 \\ \Rightarrow m\mleft(perpendicular\mright)=(-1)/(-4)=(1)/(4) \\ m\mleft(perpendicular\mright)=(1)/(4) \\ \\ \therefore m\mleft(perpendicular\mright)=(1)/(4) \end{gathered}`

The equation for the line perpendicular is given as:

`\begin{gathered} y=mx+b \\ But\colon m=m\mleft(perpendicular\mright)=(1)/(4) \\ \Rightarrow y=(1)/(4)x+b \\ (x,y)=Q(6,-1) \\ -1=(1)/(4)\cdot6+b \\ -1=(6)/(4)+b \\ -1=(3)/(2)+b \\ \text{Subtract ''}(3)/(2)\text{'' from both sides, we have:} \\ -1-(3)/(2)=b \\ -(5)/(2)=b \\ b=-(5)/(2) \\ \text{Substitute the value of ''b'' into the equation, we have:} \\ \Rightarrow y=(1)/(4)x-(5)/(2) \\ \\ \therefore The\text{ equation of a line perpendicular is }y=(1)/(4)x-(5)/(2) \end{gathered}`

Therefore, the equation of the parallel line is y = 1/4x - 5/2