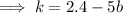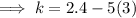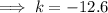Question

What is the value of K such that (x^3-2x^2+kx-12)/(x-5) has a remainder of 0

Answer 1

–12.6

Explanation:

`\frac{ \\ {x }^(3) - {2x}^(2) + kx - 12}{x - 5} = 0`

that means (x–5) is a factor of x³ – 2x² +kx – 12

since it resulted to zero according to the rules of zeros of polynomial.

x–5 = 0

x = 5

by substituting

f(x) = 5³ – 2(5)² + k(5) – 12 = 0

125 – 50 + 5k – 12 = 0

75 + 5k – 12 = 0

5k + 75 – 12 = 0

5k + 63 = 0

5k = –63

`( \\ 5k)/(5) = ( - 63)/(5)`

`k = - 12.6 \: or \: - 12 (3)/(5)`

I hope I helped

Answer 2

k = -12.6

Explanation:

Given rational polynomial:

`(x^3-2x^2+kx-12)/(x-5)`

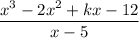
When we divide a polynomial f(x) by (x − d) the remainder is f(d).

If the remainder is zero, then (x - d) must be a factor of f(x).

If a cubic polynomial is divided by (x - d) then:

`\implies (x-d)(ax^2+bx+c)`

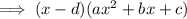
where:

• a is the leading coefficient
• -cd is the constant

If the constant of the cubic polynomial is -12 and d = 5:

`\implies -cd=-12`

`\implies -5c=-12`

`\implies c=2.4`

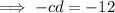
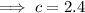
The leading coefficient of the cubic polynomial is one. Therefore:

`\implies (x-5)(x^2+bx+2.4)`

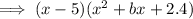
Expand and collect like terms:

`\implies x^3+bx^2+2.4x-5x^2-5bx-12`

`\implies x^3+(b-5)x^2+(2.4-5b)x-12`

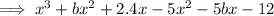
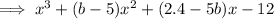
The find the value of b, compare the coefficients of the term in x²:

`\implies b-5=-2`

`\implies b=3`

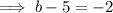
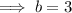
To find k, substitute the found value of b into the coefficient of x:

`\implies k=2.4-5b`

`\implies k=2.4-5(3)`

`\implies k=-12.6`