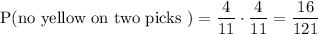Question

PLEASE HELP ASAP:

A bag has 1 speckled pen, 3 black pens,
and 7 yellow pens. You randomly pull a pen
from the bag, put it back, and then pull out
another one.
What is the probability of not getting a yellow and then not getting a yellow? Write
your answer as a fraction.

Answer 1

`\textrm{P(no yellow on two picks )} = (16)/(121)`

Explanation:

The total number of pens is 1 + 3 + 7 = 11 out of which 7 are yellow.

(We don't really care what color the other pens are since we are interested only in the yellow pens)

`\textrm{P(yellow on first pick )} = \frac{\textrm{Number of yellow pens}}{\textrm{Total number of pens}} = (7)/(11)`

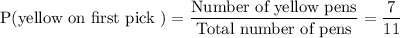
The probability of not getting a yellow on first pick is the complement of this probability and is 1 less than the probability of picking an yellow

`\textrm{P(not yellow on first pick )} = 1- (7)/(11) = (4)/(11)`

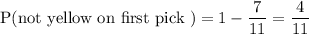
Since we are putting back the pen after the first pick, the total number of pens as well as pens of each color remain the same.

Therefore the probability of not getting a yellow on second pick is the same as the first pick and is
`(4)/(11)`

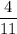
The combined probability of not getting an yellow on both picks is the product of these probabilities

`\textrm{P(no yellow on two picks )} = (4)/(11)\cdot (4)/(11) = (16)/(121)`