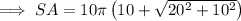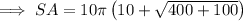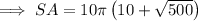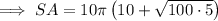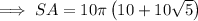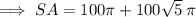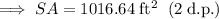Question

A cone with diameter 20 ft and a height of 20
ft.

Answer 1

Volume = 2094.40 ft³ (2 d.p.)

Surface area = 1016.64 ft² (2 d.p.)

Explanation:

If the diameter of a cone is 20 ft, then its radius is 10 ft since d = 2r.

`\boxed{\begin{minipage}{4 cm}\underline{Volume of a cone}\\\\$V=(1)/(3) \pi r^2 h$\\\\where:\\ \phantom{ww}$\bullet$ $r$ is the radius. \\ \phantom{ww}$\bullet$ $h$ is the height.\\\end{minipage}}`

Given:

• r = 10
• h = 20

Substitute the given values of r and h into the formula for the volume of a cone and solve for V:

`\implies V=(1)/(3) \pi \cdot 10^2 \cdot 20`

`\implies V=(1)/(3) \pi \cdot 100 \cdot 20`

`\implies V=(1)/(3) \pi \cdot 2000`

`\implies V=(2000)/(3) \pi`

`\implies V=2094.40\;\rm ft^3\;\;(2\;d.p.)`

`\boxed{\begin{minipage}{4 cm}\underline{Surface Area of a cone}\\\\$SA=\pi r \left(r+√(h^2+r^2)\right)$\\\\where:\\ \phantom{ww}$\bullet$ $r$ is the radius. \\ \phantom{ww}$\bullet$ $h$ is the height.\\\end{minipage}}`

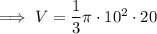
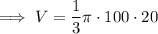
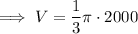
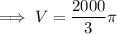
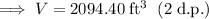
Given:

• r = 10
• h = 20

Substitute the given values of r and h into the formula for the surface area of a cone and solve for SA:

`\implies SA=10\pi \left(10+√(20^2+10^2)\right)`

`\implies SA=10\pi \left(10+√(400+100)\right)`

`\implies SA=10\pi \left(10+√(500)\right)`

`\implies SA=10\pi \left(10+√(100\cdot 5)\right)`

`\implies SA=10\pi \left(10+10√(5)\right)`

`\implies SA=100\pi +100√(5)\: \pi`

`\implies SA=1016.64\; \rm ft^2\;\;(2\;d.p.)`