Answer:

Explanation:
Method 1
To find the scale factor of the dilation of a figure, simply divide the x-value (or y-value) of a vertex of the dilated image Q'R'S'T' by the x-value (or y-value) of the corresponding vertex of the pre-image QRST.
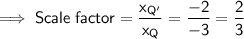
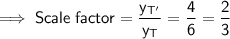
Therefore, the scale factor is 2/3.
Method 2
To find the scale factor of the dilation of a figure, first find the lengths of corresponding sides using the distance formula.

From inspection of the given diagram:
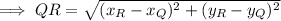
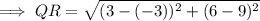
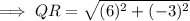
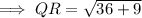
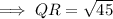
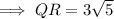
From inspection of the given diagram:
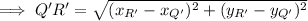
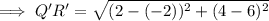
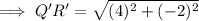
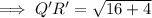
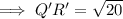
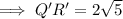
To find the scale factor of dilation that maps QRST onto Q'R'S'T', divide the length of Q'R' by the length of QR:
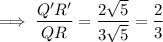
Therefore, the scale factor is 2/3.