Question

A skater is initially spinning at a rate of 13.0 rad/s with a rotational inertia of 3.20 kg·m2 when her arms are extended. What is her angular velocity after she pulls her arms in and reduces her rotational inertia to 1.60 kg·m2? rad/s

Answer 1

Given data:

* The initial angular velocity of the skater is,

`\omega_1=13\text{ rad/s}`

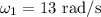
* The initial rotational inertia of her arm is,

`I_1=3.2kgm^2`

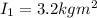
* The final rotational inertia of her arm is,

`I_2=1.6kgm^2`

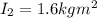
Solution:

As the angular momentum of the system remains conserved before and after extending the arms, thus,

`\begin{gathered} L_1=L_2 \\ I_1\omega_1=I_2\omega_2 \end{gathered}`

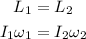
Substituting the known values,

`\begin{gathered} 3.2*13=1.6*\omega_2_{} \\ 41.6=1.6*\omega_2 \\ \omega_2=(41.6)/(1.6) \\ \omega_2=26\text{ rad/s} \end{gathered}`

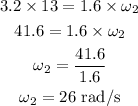
Thus, the angular velocity of the skater is 26 rad/s.