Question

Solve 2 log x = log 64.
x= 1.8
x=8
x= 32
x=128

Answer 1

x = 8

Explanation:

Given expression:

`2\log x=\log 64`

`\textsf{Apply the log power law}: \quad n\log x=\log x^n`

`\implies \log x^2=\log 64`

Rewrite 64 as 8²:

`\implies \log x^2=\log 8^2`

`\textsf{Apply the log equality law}: \quad \textsf{If\;\;$\log x=\log y$\;\;then\;\;$x=y$}`

`\implies x^2=8^2`

Square root both sides:

`\implies x=8`

Answer 2

x=8.

Explanation:

1. Write the expression.

`2log(x)=log(64)`

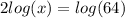
2. Divide both sides of the equation by "2".

`(2log(x))/(2) =(log(64))/(2)\\ \\log(x)=(log(64))/(2)`

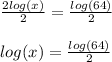
3. Apply number "10" as the base of an exponent of each side of the equation.

When a logarithm doesn't have it's base expressed (base is tipically written as a subscript) we can assume it'sbase is 10. Therefore, to solve this equation, take the following step:

`10^(log(x)) =10^{(log(64))/(2)} \\ \\x=10^{(log(64))/(2)}\\ \\x=8`

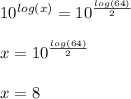
4. Verify the answer.

If the result is correct, then the equation should return the same value of both sides of the equal symbol (=) when we substitute the variable "x" by it's calculated value, 8.

`2log(8)=log(64)\\ \\1.806179974=1.806179974`

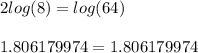
As you can tell, the same number appears on both sides of the equal symbol, this means that the result is correct!