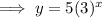Question

NO LINKS!!! Part 3

Find an exponential function y = ab^x form that satisfies the given information

f. passes through (-1, 72.73) and (3, 106.48)

g. passes through (-2, 351.56225) and (3, 115.2)

h. passes through (4, 405) and (9, 98415)

Answer 1

`\text{f)} \quad y=80(1.1)^x`

`\text{g)} \quad y=225(0.8)^x`

`\text{h)} \quad y=5(3)^x`

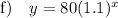
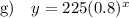
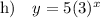
Explanation:

`\boxed{\begin{minipage}{9 cm}\underline{General form of an Exponential Function}\\\\$y=ab^x$\\\\where:\\\phantom{ww}$\bullet$ $a$ is the initial value ($y$-intercept). \\ \phantom{ww}$\bullet$ $b$ is the base (growth/decay factor) in decimal form.\\\end{minipage}}`

Part (f)

Given points:

• (-1, 72.73)
• (3, 106.48)

Substitute the given (x, y) points into the exponential function formula to create two equations:

`\implies 72.73=ab^(-1)`

`\implies 106.48=ab^3`

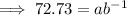
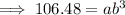
Divide the second equation by the first equation to eliminate a:

`\implies (106.48)/(72.73)=(ab^3)/(ab^(-1))`

`\implies (106.48)/(72.73)=(b^3)/(b^(-1))`

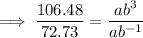
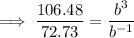
Solve for b:

`\implies (106.48)/(72.73)=b^3 \cdot b^(1)`

`\implies (106.48)/(72.73)=b^(3+1)`

`\implies (106.48)/(72.73)=b^4`

`\implies b=1.09998968...`

`\implies b=1.1`

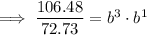
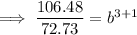
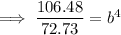
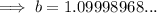
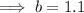
Substitute the found value of b into one of the equations and solve for a:

`\implies 72.73=a \cdot (1.09998968...)^(-1)`

`\implies a=80.0022499...`

`\implies a=80`

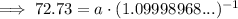
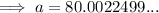
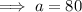
Substitute the found values of a and b into the exponential function formula:

`\implies y=80(1.1)^x`

---------------------------------------------------------------------------------------

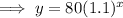
Part (g)

Given points:

• (-2, 351.56225)
• (3, 115.2)

Substitute the given (x, y) points into the exponential function formula to create two equations:

`\implies 351.56225=ab^(-2)`

`\implies 115.2=ab^3`

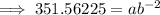
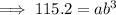
Divide the second equation by the first equation to eliminate a:

`\implies (115.2)/(351.56225)=(ab^3)/(ab^(-2))`

`\implies (115.2)/(351.56225)=(b^3)/(b^(-2))`

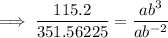
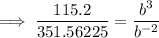
Solve for b:

`\implies(115.2)/(351.56225)=b^3 \cdot b^(2)`

`\implies (115.2)/(351.56225)=b^(3+2)`

`\implies (115.2)/(351.56225)=b^5`

`\implies b=0.800000113...`

`\implies b=0.8`

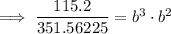
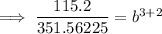
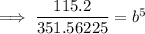
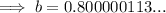
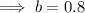
Substitute the found value of b into one of the equations and solve for a:

`\implies 115.2=a(0.800000113...)^3`

`\implies a=224.999904`

`\implies a=225`

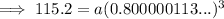
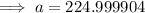
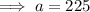
Substitute the found values of a and b into the exponential function formula:

`\implies y=225(0.8)^x`

---------------------------------------------------------------------------------------

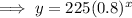
Part (h)

Given points:

• (4, 405)
• (9, 98415)

Substitute the given (x, y) points into the exponential function formula to create two equations:

`\implies 405=ab^4`

`\implies 98415=ab^9`

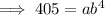
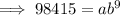
Divide the second equation by the first equation to eliminate a:

`\implies (98415)/(405)=(ab^9)/(ab^4)`

`\implies 243=(b^9)/(b^4)`

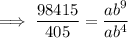
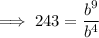
Solve for b:

`\implies 243=b^9 \cdot b^(-4)`

`\implies 243=b^(9-4)`

`\implies 243=b^(5)`

`\implies b=3`

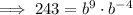
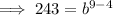
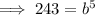
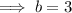
Substitute the found value of b into one of the equations and solve for a:

`\implies 405=a \cdot 3^4`

`\implies 81a=405`

`\implies a=5`

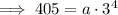
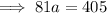
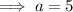
Substitute the found values of a and b into the exponential function formula:

`\implies y=5(3)^x`