Question

NO LINKS!! Part 1

Find an exponential function in y = ab^x form that satisfies the given information :

a. Has y-int (0, 2) and has a multiplier of 0.8

b. passes through the points (0, 3.5) and (2, 31.5)

Answer 1

`\textsf{a)} \quad y=2(0.8)^x`

`\text{b)} \quad y=3.5(3)^x`

Explanation:

`\boxed{\begin{minipage}{9 cm}\underline{General form of an Exponential Function}\\\\$y=ab^x$\\\\where:\\\phantom{ww}$\bullet$ $a$ is the initial value ($y$-intercept). \\ \phantom{ww}$\bullet$ $b$ is the base (growth/decay factor) in decimal form.\\\end{minipage}}`

Question (a)

Given:

• y-intercept = (0, 2) ⇒ a = 2
• multiplier = 0.8 ⇒ b = 0.8

Substitute the values of a and b into the exponential function formula:

`\implies y=2(0.8)^x`

Question (b)

The y-intercept is when x = 0. Therefore, given the function passes through point (0, 3.5), the y-intercept is 0.35 ⇒ a = 3.5.

Substitute the found value of a and given point (2, 31.5) into the exponential function formula and solve for b:

`\implies 31.5=3.5b^2`

`\implies b^2=9`

`\implies b=3`

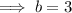
Substitute the values of a and b into the exponential function formula:

`\implies y=3.5(3)^x`

Answer 2

• A) y = 2*0.8ˣ
• B) y = 3.5*3ˣ

-----------------------------------------

Part A

Use the coordinates to determine the function.

Point (0, 2):

• 2 = a*b⁰ ⇒ 2 = a

The function becomes:

• y = 2bˣ

It has a multiplier of 0.8, so b = 0.8, so the function is:

• y = 2*0.8ˣ

Part B

Use the first point:

• 3.5 = a*b⁰ ⇒ 3.5 = a

Use the second point:

• 31.5 = 3.5*b²
• 9 = b²
• b = √9
• b = 3

The function is:

• y = 3.5*3ˣ