Question

Simplify: 14 root 20 minus -3 root 125

Answer 1

I assumed that the square roots were not nested for this problem, which means I put √125 beside √20 - (-3).

70√115

Explanation:

Start this problem off by applying an inversive rule: x - (-y) = x + y

`=14√(20+3)√(125)`

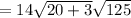
Now, simplify √125 into a radical.

`= \sqrt[5]{5}`

Now that the previous number is a radical, this is what the expression should look like:

`=14√(20+3)* 5√(5)`

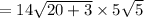
Next, we multiply the numbers together. Borrow the ^5 from the radical, then regroup like terms.

`14* 5 = 70\\=70√(20+3)√(5)\\=70√(5)\:* √(20+3)`

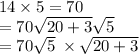
Last of all, we must apply the radical rule, which states that if there are two radicals, radical X and radical Y, these radicals will combine into one, and then will be multiplied by each other. However, note that the radicals cannot equal 0.

`√(5)√(23)=√(5* 23)`

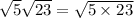
Now, since the radicals are combined, multiply them together. 5 times 23 is 115, so combine the square root, and that will be your final answer. :)

Hope this helps!