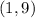
1) Since g(x) is displayed in a table, let's find which rule g(x) has by picking two points: (-2,3), (-1,5) let's find the slope between those points:
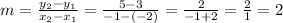
So, the slope is 2. Note that in the table we can see the point (0,7) so we can tell the y-intercept is 7. And the rule is:
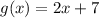
2) Now, let's equate f(x) to g(x) and find the x coordinate of the shared point:
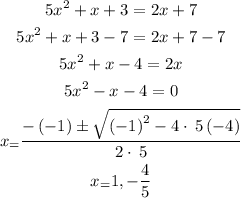
The next step is to plug and check. So let's plug x=1 into each original equation. The true solution(s) will yield the same output.
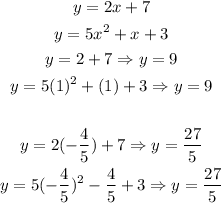
Thus, the answer is the point
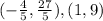
As there is only one answer in the choices we can tell that the answer is:
(1,9)