Question

What is a solution to the system of equations that includes quadratic function f(x) and linear function g(x)?f(x) = 5x2 + x + 3xg(x)–23–150719211 (-1, 7) (0, 3) (0, 7) (1, 9)

Answer 1

(1, 9)

Explanation:

I got it right on the test.

Answer 2

`(1,9)`

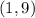
1) Since g(x) is displayed in a table, let's find which rule g(x) has by picking two points: (-2,3), (-1,5) let's find the slope between those points:

`m=(y_2-y_1)/(x_2-x_1)=(5-3)/(-1-(-2))=(2)/(-1+2)=(2)/(1)=2`

So, the slope is 2. Note that in the table we can see the point (0,7) so we can tell the y-intercept is 7. And the rule is:

`g(x)=2x+7`

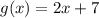
2) Now, let's equate f(x) to g(x) and find the x coordinate of the shared point:

`\begin{gathered} 5x^2+x+3=2x+7 \\ 5x^2+x+3-7=2x+7-7 \\ 5x^2+x-4=2x \\ 5x^2-x-4=0 \\ x_=(-\left(-1\right)\pm√(\left(-1\right)^2-4\cdot\:5\left(-4\right)))/(2\cdot\:5) \\ x_=1,-(4)/(5) \end{gathered}`

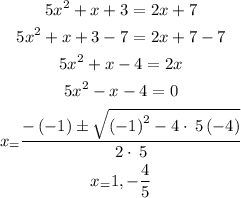
The next step is to plug and check. So let's plug x=1 into each original equation. The true solution(s) will yield the same output.

`\begin{gathered} y=2x+7 \\ y=5x^2+x+3 \\ y=2+7\Rightarrow y=9 \\ y=5(1)^2+(1)+3\Rightarrow y=9 \\ \\ y=2(-(4)/(5))+7\Rightarrow y=(27)/(5) \\ y=5(-(4)/(5))^2-(4)/(5)+3\Rightarrow y=(27)/(5) \end{gathered}`

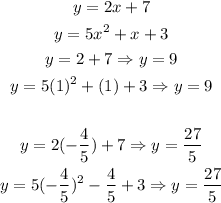
Thus, the answer is the point

`(-(4)/(5),(27)/(5)),(1,9)`

As there is only one answer in the choices we can tell that the answer is:

(1,9)