Question

NO LINKS!!

$940 has been put into an investment account that grows at 5.14% compounded semi-annually. (NOT MULTIPLE CHOICE)

a. Create a table that shows this growth
b. Write an equation that models this situation
c. State what x represents in your equation
d. State what y represents in your equation
e. How much will in the account after 12 years?

Answer 1

a) See below.

`\textsf{b)} \quad y=940\left(1.0257\right)^(2x)`

c) x is the number of years.

d) y is the account balance in dollars.

e) $1728.29

Explanation:

Part (a)

Interest is compounded semi-annually, so:

• 5.14% ÷ 2 = 2.57%

Therefore, calculate 1.0257% of the balance every 6 months:

`\begin{array}\cline{1-2} \vphantom{\frac12} \rm Years& \rm Account\;balance\;(\$) \\\cline{1-2} \vphantom{\frac12} 0& 940.00\\\cline{1-2} \vphantom{\frac12} 0.5& 964.16\\\cline{1-2} \vphantom{\frac12} 1& 988.94\\\cline{1-2} \vphantom{\frac12} 1.5&1014.35\\\cline{1-2} \vphantom{\frac12} 2&1040.42\\\cline{1-2} \vphantom{\frac12} 2.5&1067.16\\\cline{1-2} \vphantom{\frac12} 3&1094.59\\\cline{1-2} \end{array}`

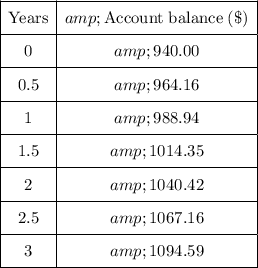
Part (b)

An equation that models this situation is:

`\implies y=940\left(1+(0.0514)/(2)\right)^(2x)`

`\implies y=940\left(1.0257\right)^(2x)`

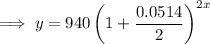
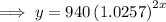
Part (c)

x is the number of years.

Part (d)

y is the account balance in dollars.

Part (e)

To calculate how much will be in the account after 12 years, substitute x = 12 into the equation from part (b):

`\implies y=940\left(1.0257\right)^(2 * 12)`

`\implies y=940\left(1.0257\right)^(24)`

`\implies y=940\left(1.8386054...\right)`

`\implies y=1728.2890...`

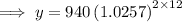
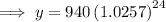
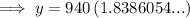
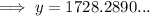
Therefore, $1728.29 will be in the account after 12 years.