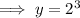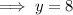Question

NO LINKS!!!!

1. A savings account starts with $720 and earns an annual rate of 4.8%. Write an equation and find the amount of money in the account for 12 years.

Equation:
Solution


2. Bacteria can multiply at an alarming rate when each bacteria splits into two new cells , thus doubling. If we start with only one bacteria, which can double, how many bacteria will we have be the end of 3 days?

Equation:
Solution:

Answer 1

`\textsf{1.\;\;Equation:\quad$A=720(1.048)^(t)$}`

`\textsf{Solution:\quad$\$1263.77$}`

`\textsf{2.\;\;Equation:\quad$y=2^x$}`

`\textsf{Solution:\quad$8$}`

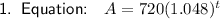
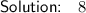
Explanation:

Question 1

Assuming the account earns annual compound interest.

`\boxed{\begin{minipage}{7 cm}\underline{Annual Compound Interest Formula}\\\\$ A=P\left(1+r\right)^(t)$\\\\where:\\\\ \phantom{ww}$\bullet$ $A =$ final amount \\ \phantom{ww}$\bullet$ $P =$ principal amount \\ \phantom{ww}$\bullet$ $r =$ interest rate (in decimal form) \\ \phantom{ww}$\bullet$ $t =$ time (in years) \\ \end{minipage}}`

Given values:

• P = $720
• r = 4.8% = 0.048

Substitute the given values or P and r into the annual compound interest formula to create an equation for the amount of money in the account after t years:

`\implies A=720(1+0.048)^(t)`

`\implies A=720(1.048)^(t)`

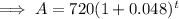
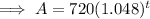
To find the amount of money in the account after 12 years, substitute t = 12 into the equation:

`\implies A=720(1.75523549...)`

`\implies A=1263.76955...`

`\implies A=1263.77`

---------------------------------------------------------------------------------

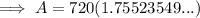
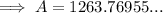
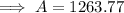
Question 2

`\boxed{\begin{minipage}{9 cm}\underline{General form of an Exponential Function}\\\\$y=ab^x$\\\\where:\\\phantom{ww}$\bullet$ $a$ is the initial value ($y$-intercept). \\ \phantom{ww}$\bullet$ $b$ is the base (growth/decay factor) in decimal form.\\\end{minipage}}`

Given values:

• a = 1 (initial number of bacteria)
• b = 2 (as the bacteria doubles)

Substitute the given values or a and b into the exponential function formula to create an equation for the number of bacteria after x days:

`\implies y=1(2)^x`

`\implies y=2^x`

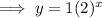
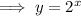
To find the number of bacteria after 3 days, substitute x = 3 into the equation:

`\implies y=2^3`

`\implies y=8`