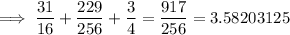Question

Computer the lower Riemann sum for the given function f(x) = 4 - x^3 over the interval x E [0,1] with respect to the partition P = [0, 1/2, 3/4, 1]

Answer 1

`(917)/(256)=3.58203125`

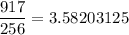
Explanation:

The Riemann sum is a method by which we can approximate the area under a curve using a series of rectangles.

The Lower Riemann Sum uses the minimum height of the rectangle on each subinterval.

As the Lower Riemann Sum is entirely below the curve, it is an underestimation of the area under the curve.

The number of partitions is the number of rectangles used.

Partitions can be of equal length or not of equal length.

Given:

• Function: f(x) = 4 - x³
• Interval: [0, 1]
• Partition, P = [0, 1/2, 3/4, 1]

The given partition divides the interval [0, 1] into 3 subintervals:

• [0, 1/2], [1/2, 3/4] and [3/4, 1]

To calculate the areas of the rectangles, multiply the width of each rectangle by its height.

The width is the difference between the x-values of each subinterval.

The height is the minimum value of the function across the subinterval. For the given function, this is the value of the function for the right side of the subinterval.

First rectangle [0, 1/2]:

`\begin{aligned}\implies \left((1)/(2)-0\right) \cdot f\left((1)/(2)\right)&=(1)/(2) \cdot \left(4-\left((1)/(2)\right)^3\right)\\\\&=(1)/(2) \cdot (31)/(8)\\\\&=(31)/(16)\end{aligned}`

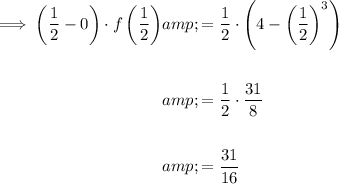
Second rectangle [1/2, 3/4]:

`\begin{aligned}\implies \left((3)/(4)-(1)/(2)\right) \cdot f\left((3)/(4)\right)&=(1)/(4) \cdot \left(4-\left((3)/(4)\right)^3\right)\\\\&=(1)/(4) \cdot (229)/(64)\\\\&=(229)/(256)\end{aligned}`

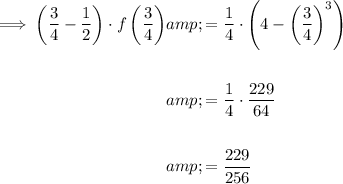
Third rectangle [3/4, 1]:

`\begin{aligned}\implies \left(1-(3)/(4)\right) \cdot f\left(1\right)&=(1)/(4) \cdot \left(4-\left(1\right)^3\right)\\\\&=(1)/(4) \cdot 3\\\\&=(3)/(4)\end{aligned}`

Therefore, the Lower Reimann Sum for the given function over the given interval and partitions is the sum of the area of the rectangles:

`\implies (31)/(16)+(229)/(256)+(3)/(4)=(917)/(256)=3.58203125`