Question

Find the intervals on which f is increasing or decreasing, and find the local maximumand minimum values of f.
`f(x) = x + (4)/(x^2)`Now I know the first derivative is
`f'(x) = 1 - (8)/(x^3)` but I don't know how to get the critical points

Answer 1

Given the function f(x) defined as:

`f(x)=x+(4)/(x^2)`

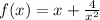
Taking the derivative of the function:

`f^(\prime)(x)=1-(8)/(x^3)`

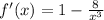
Now, we calculate the critical points using the equation:

`\begin{gathered} f^(\prime)(x)=0 \\ 1-(8)/(x^3)=0 \\ 1=(8)/(x^3) \\ x^3=8 \\ x=2 \end{gathered}`

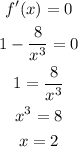
Now, we explore the intervals of increasing and decreasing for f(x) using the critical point, taking into account the discontinuity in x = 0:

`\begin{gathered} x>2\colon f^(\prime)(x)>0\text{ (Increasing)} \\ 00\text{ (Increasing)} \end{gathered}`

The intervals are:

`\begin{gathered} \text{Increasing}\colon(-\infty,0)\cup(2,\infty) \\ \text{Decreasing}\colon(0,2) \end{gathered}`

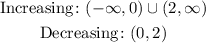
The function has a local minimum at x = 2, because f''(2) > 0. There is no local maximum.