Answer:
a) 98m , b) 89m
Explanation:
(a) Given,
- The area of a rectangular parking lot is 8428 m²
- width of the parking lot is 86 m
To Find : Length of the Parking lot
Length of a rectangle shape can be derived by the formula,

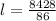

Hence , the length of a rectangular parking lot is 98m
(b) Given ,
- The perimeter of a rectangular pool is 376 m
- length of the pool is 99 m
To Find : The width of the rectangular pool
We take the width as variable 'x'
Now we plug it into the perimeter of a rectangle equation

Using distributive property we,
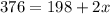
We now flip the equation
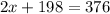
 ( Transposing into the right hand side)
( Transposing into the right hand side)

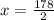
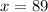

Hence , the width of the rectangular swimming pool is 89m