Question

PLS HELP 100 POINTS

The function f(x) = x + 3 represents the length of a rectangle, and the function g(x) = 6x − 5 represents the width of the rectangle. What is the area of the rectangle if x = 3?

−72
19
78
117

Answer 1

x = 3
Sub in 3 for x

x +3
3+3 = 6 (length)

6x-5
6(3)-5 = 13 (width)

Length x Width = Area
6 x 13 = 78

Answer 2

78 square units

Explanation:

Length of the rectangle:

• 
  `f(x)=x+3`

Width of the rectangle:

• 
  `g(x)=6x-5`

The area of a rectangle can be calculated by multiplying the length by the width. Therefore, the equation for the area of the rectangle with the given length and width is:

`\begin{aligned}\implies \textsf{Area}&=\sf length * width\\& = f(x) \cdot g(x)\\&=(x+3)(6x-5)\\&=6x^2-5x+18x-15\\&=6x^2+13x-15\end{aligned}`

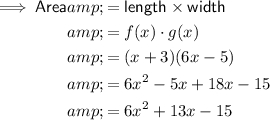
To find the area of the rectangle if x = 3, substitute x = 3 into the found equation:

`\begin{aligned}\implies \textsf{Area}&=6x^2+13x-15\\&=6(3)^2+13(3)-15\\&=6(9)+13(3)-15\\&=54+39-15\\&=93-15\\&=78\;\; \sf square \; units\end{aligned}`

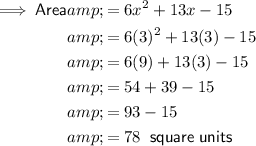
Therefore, the area of the rectangle is 78 square units.