Answer:
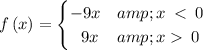
Explanation:
The first thing to note is that absolute value functions are piecewise functions.
A piecewise function is a function in which more than one formula is used to define the output over different pieces of the domain or inputs(in this case the x-values).
In this case, the absolute value function is
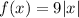
To write this function as a piecewise function you have to use the definition of
 :
:
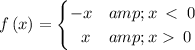
Applying this to
 we multiply each of the parts by 9 to get
we multiply each of the parts by 9 to get
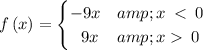
At
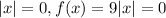
The graph of the function is attached for easier understanding