Question

Let L be the line through A = (1, 2,−1) and B = (5,−3, 4).

Answer the following questions below:
1. Find a direction vector of L
2. Find a parameterization of L.
3. Find the two points on L that are at distance 2 away from A.
4. Find a unit speed parameterization of L.

Answer 1

1. (4, -5, 5)
2. L = (1+4t, 2-5t, -1+5t)
3. (1+4√66/33, 2-5√66/33, -1+5√66/33), (1-4√66/33, 2+5√66/33, -1-5√66/33)
4. (1-2t√66/33, 2+5√66/66, -1-5√66/66)

Explanation:

Given L is the line through A(1, 2, -1) and B(5, -3, 4), you want its direction vector, a parameterization of L, 2 points on L that are 2 units from A, and a unit speed parametrization of L.

1. Direction vector

A direction vector for L will be the vector AB.

`\overrightarrow{AB}=B-A=(5,-3,4)-(1,2,-1)\\\\\boxed{\overrightarrow{AB}=(4, -5,5)}`

2. Parameterized line

The parameterized equation will be ...

`L=A+t\cdot\overrightarrow{AB}\\\\\boxed{L=(1+4t,2-5t,-1+5t)}`

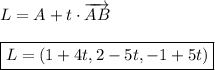
3. Distance 2

The direction vector has length √66, so we can find two points on L that are 2 units from A by using t = ±2/√66 in the parameterized equation.

Here, they are:

P1 = L(2/√66) = (1 +8/√66, 2 -10/√66, -1 +10/√66)

P2 = L(-2/√66) = (1 -8/√66, 2 +10/√66, -1 -10/√66)

In the Answer section above, these are written with rationalized denominators.

4. Unit speed

The unit speed parametrization uses the unit direction vector instead of the unnormalized direction vector in the parameterized equation. Effectively, t is scaled by a factor of 1/√66.

L = (1 +4t/√66, 2 -5t/√66, -1 +5t/√66)

In the Answer section above, this is written with rationalized denominators.

You might notice here that it is easier to answer part 3 if you have this equation. You need only substitute t=±2 to get the points 2 units from A.