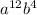Answer:
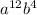
Explanation:
To simplify we will have to use the negative exponent rule and the power rule along with some algebra.
Negative Exponent Rule
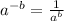
Power Rule
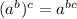
Given
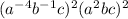
Rewrite
 using negative exponent rule.
using negative exponent rule.
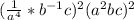
Rewrite
 using negative exponent rule.
using negative exponent rule.
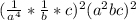
Simplify
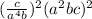
Rewrite the base as its reciprocal.
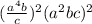
Apply the power rule.
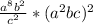
Apply the power rule.
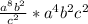
Cancel the common factor of
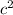 .
.
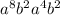
Apply the power rule.