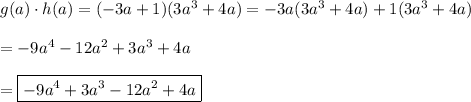Question

Can someone help with this? Please be right

Answer 1

See attached

Explanation:

You want various combinations of the functions g(a) = -3a+1 and h(a) = 3a³ +4a.

g/h

The functions have no common factors, so their ratio leaves the function expressions unchanged:

`(g(a))/(h(a))=\boxed{(-3a+1)/(3a^3+4a)}`

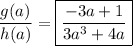
h+g

The like terms are combined when the functions are added.

`h(a)+g(a)=(3a^3+4a)+(-3a+1)=3a^3+(4-3)a+1\\\\=\boxed{3a^3+a+1}`

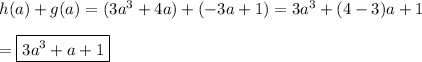
g-h

Similarly, the like terms are combined when the functions are subtracted.

`g(a)-h(a)=(-3a+1)-(3a^3+4a)=-3a^3+(-3-4)a+1\\\\=\boxed{-3a^3-7a+1}`

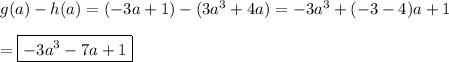
g·h

The product is found the way products are usually found. Each term of one of the factors is multiplied by each term of the other factor, and these products are summed. You can think of it as repeated application of the distributive property.

`g(a)\cdot h(a)=(-3a+1)(3a^3+4a)=-3a(3a^3+4a)+1(3a^3+4a)\\\\=-9a^4-12a^2+3a^3+4a\\\\=\boxed{-9a^4+3a^3-12a^2+4a}`